
1. Cartesian Coordinate
System: Before we can talk about verbogeometry, we
must have a look of some pertinent elements in analytic geometry.
Concerning this paper on verbogeometry, you should know enough
analytic geometry to plot points and a few basic equations on
a Cartesian coordinate system. However, I would like to believe
that anyone should be able to enjoy some understanding of verbogeometry.
If you need a refresher on the Cartesian coordinate system, you
may want to look online. Wikipedia has a nice overview of the System.
When we look at the two-dimensional axis of a Cartesian coordinate
system, we can see that by picking a point somewhere on the plane
defined by this axis that there is a relationship of this point
back to the origin. This relationship is understood by the nomenclature
of the coordinate pair (x,y) where x and y are distances along
each axis from the origin. Furthermore, if we draw lines from
a newly created point, perpendicular to both the x-axis and the
y-axis and taking into consideration the axis system in the background
then we will make a rectangle. (See figure. 1)
Figure. 1
The area of a rectangle is product of the lengths of its sides and in the upcoming example the product of the values for the x and y coordinates of this point. Of course this one is a special case because we used the axis origin as our starting point. Example: Let us arbitrarily pick a point defined by the x-y coordinates of (11,13) and draw lines perpendicular to the axes to illuminate what I just said. The area of any rectangle is equal to its height multiplied by its base (The product of the lengths of its sides). We have a green rectangle delineated on our axis system. (See figure. 1) The height of our rectangle is 13 units and it base it 11 units. The area of our rectangle is 143 square units … or 13 X 11 = 143
This later example is one of pure mathematics. However if we want
to use math as a language then we will have to apply concepts
or words to our axis system.
Let us look at a typical physics problem of distance, velocity
and time displayed on a two dimensional axis system. Let us assign
the y-axis to be levels of velocity in units of miles per hour
and the x-axis to be amounts of time in units of hours. (See figure.
2)
Figure 2 
The distance of an object traveling in space
is equal to the velocity of the object multiplied by the average
time it is traveling in space or d=vt. Let us use the same pure
mathematical example as before but by our contextualizing the
axis and assigning the y-axis to represent velocity and the x-axis
to represent time, our original point from the last example (11,13)
has a new meaning. To reiterate … the point before was in
the realm of pure mathematics but now the point represents a moment
in time of a speeding object. The object is traveling 13 miles
per hour and has been traveling for 11 hours. So to calculate,
(d = vt), the distance the object has traveled we must multiply
the velocity by the time or 13 miles per hour times 11 hours which
equals 143 miles.
In essence, what we have done has been to assign a concept by
using words (velocity and time) to our axis system. Moving our
attention up or down on the y-axis displays different values of
velocity. Moving left and right on, the x-axis displays different
amounts of duration or time. Physical experimentation can easily
verify the veracity of this equation. In addition, the same experimentation
verifies the verbal concepts and their relationship to each other
that we have assigned to our axis system. We can see the relationship
between the concepts of distance, velocity and time spread out
on a two-dimensional plane via our axis system. It is important
to note that these concepts occupy orthogonal spaces as well as
all equations in the form of A = BC. Furthermore, the equation
makes sense again because it matches our perceptions of the event
and the axis system is a model of our experience. Although the
use of the latter equations was for the purpose of denotation,
Verbogeometry is more interested in the use of equations for connotation
and witnessing dissimilar concepts forced into orthogonal spaces
to create metaphor.
2. The Mechanics of Verbogeometry:
2.1. Word-Axes and Word-Planes. One of the tenets of Verbogeometry and Mathematical
poetry is that you "calculate" values of quality as
if they were quantity. Of course this seems to be nonsense but
then one must realize that paradox is the mathematical structure
of metaphor. When quality and quantity are synonymous then the
math equations automatically transcend the normal duty of denotation
and enter into the realms of connotation. This concept also bears
some relationship to different concepts of infinity pioneered
by the Russian-German Mathematician Georg Cantor, namely the infinities
in gradation relative to the infinities in Counting.
Another tenet of verbogeometry is that it recognizes antonyms
in only a few varieties. A simple antonym is a word whose antonym
is a direct negation. (Example: just / unjust, probable / improbable
or fertile / infertile etc.) A complex antonym is a word whose
antonym is not a direct negation. (Example: just / unfair, probable
/ doubtful or fertile / barren etc.) There are also gradable (gradient)
antonyms which are pairs that express relationships in a continuum,
such as up and down. Complementary antonyms are pairs that express
an either/or relationship, such as dead or alive. Verbogeometry
uses all antonyms as if they were gradable. It is easy to find
examples where poets use complementary antonyms as if they were
gradable to create certain metaphors. Example: "Bob showed
up half dead to work today."
Within the boundaries of verbogeometry is important to understand
that we view words as objects floating in space. When we focus
on single words, with no context, they are alone inert relating
to no other words. However, when we focus on words that have a
synonymous partner we can easily imagine a line in space between
the words. Probable and improbable are good examples of simple
antonyms that we can view connected by a line. (See figure. 3)
Figure. 3 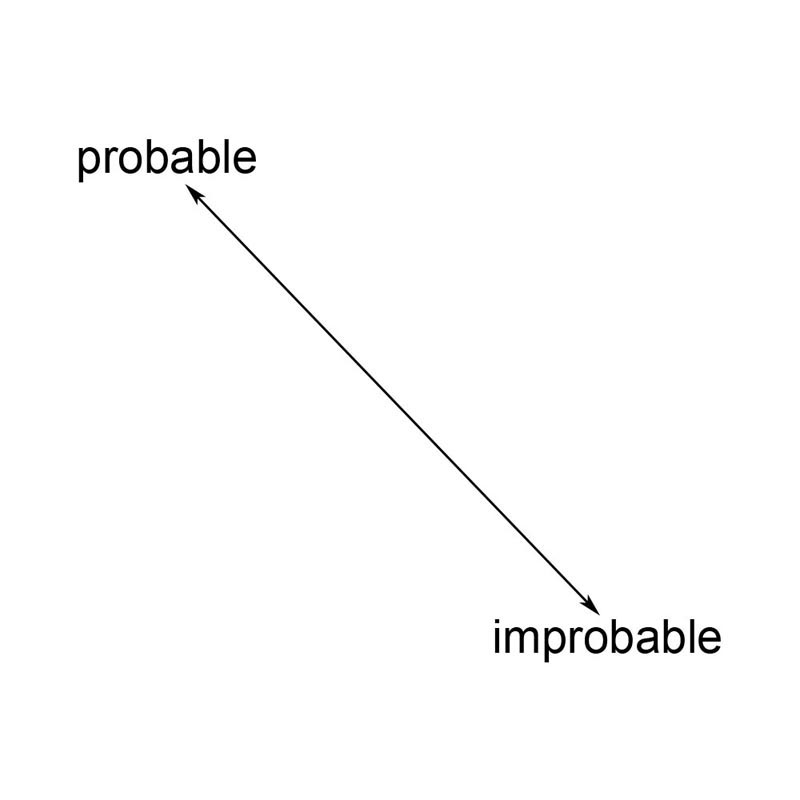
Life is full of dualities it is hard to think about qualities without thinking about opposing ideas. We can view our 'probable / improbable' one-dimensional line as a number line but instead of values of numbers on the line, we think in terms about having different levels of meaning between the two words residing at each end of the line. Due to a number-line being a one dimensional axis it is easy to visualize a word-axis as an axis for a single spatial dimension. We call any pair of words connected by a line a word-axis. Two perpendicular number lines or word axes make a two-dimensional word-axis as well as defining a word-plane. We also have the ability to view the word-plane as an infinite number of coordinates delineated by the word-pairs much like the infinite number of coordinate pairs contained within a Cartesian coordinate system described in the realm of analytic geometry.
Figure 4 
Figure 4 shows a visualization for the physics equation; distance = velocity multiplied by the time. Notice that the y axis displays velocity and the x axis displays time. When we multiply and blend the words in an infinitesimal weave, we arrive at the concept of distance in a tessellated product of the concepts of velocity and time. In another words by positioning the two axes perpendicular to each other, we view every value on one word-axis in relation to every value on the other word-axis. This method affords us a way to 'feel' the entire word plane or axis system with all its different augmented values and gradations. When we multiply two word-axes together we conceptually tessellate a two dimensional plane with different semantic values of the two words blended and augmented. If we were to take a normal Cartesian coordinate system and multiply the x positive integers (1 through 12) times the y positive integers (1 through 12) we get a tessellated plane as in Figure 5 (see figure. 5) (notice the intensity of blue relative to the value of the numbers)
Figure. 5 
To help us further visualize this concept let us create a word axis using the words red and green. In this instance, we are going to use red and green as nouns instead of adjectives. (We will use colors as adjectives later) Let us multiply a red-green axis times another red-green axis and view it visually. (See figure. 6) Multiplication of colors is similar to color addition except the disparate intensities of the colors are greater and follow a similar pattern shown in figure 5. The value of the 'numbers' is subjective and not as important as the relationship between the 'numbers'.
Figure. 6 
Figure 6 helps us to visualize different word
meanings spread across a word plane.
Let us create another example using two different word-axes. However,
let's use two different colored word axes instead of both axes
being the same colors like our previous example. Then let us break
down what we have just accomplished and look at the axes separately.
After that we will superimpose a set of different word-axes upon
our color axes to compare how the system works.
To facilitate visualizing two different word axes lets look at
an example with the word-axes red-green and blue-orange multiplied
by each other and mapped on a Cartesian coordinate system. (See
figure. 7)
Figure. 7 
(Note these diagrams are visual aids not scientific data)
Figure 7 is comprised of two axes: a red-green in the vertical and a blue orange in the horizontal. Let us look at the red-green vertical axis separately (See figure. 8)
Figure. 8 
and separate from figure 7. the blue-orange horizontal axis as well (See figure. 9)
Figure. 9 
Furthermore, notice the direction of the gradations.
When we place the axes perpendicular to each other and multiply
them together, we see the color tessellations of the word-plane.
(See figure. 7)
What is nice about using colors for our examples is that words
used for colors function as both a noun and an adjective depending
on our intent. When we map a word plane with word-axes that comprise
colors and we use them as adjective synonyms, then this word-plane
serves as a paradigm or a pedagogical tool to serve as a general
model for understanding all two axes synonym word-planes. Example:
Let create a word-plane using the two word-axes of noble/ignoble
and just/unjust. (See figure. 10)
Figure.10 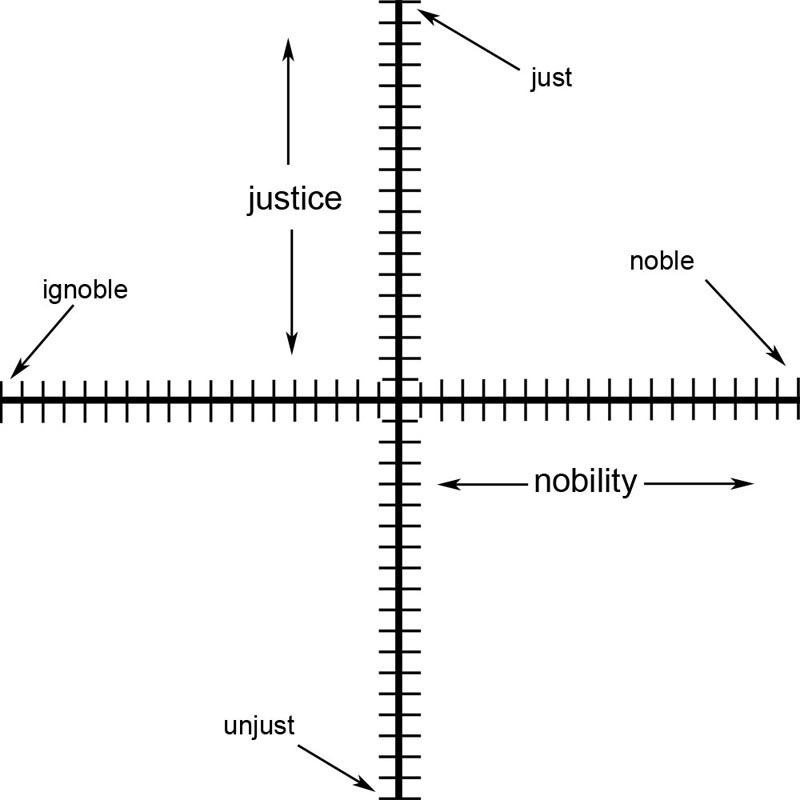
The next step would be to superimpose the noble/ignoble; just/unjust word-plane onto our previous word-plane of blue/orange; red/green. In essence, we are pretending color blue to mean ignoble, orange to mean noble, red to mean just and green to mean unjust. Now we can see the meanings blend into each other in the different areas of our word-plane.(Seefigure.11)
Figure.11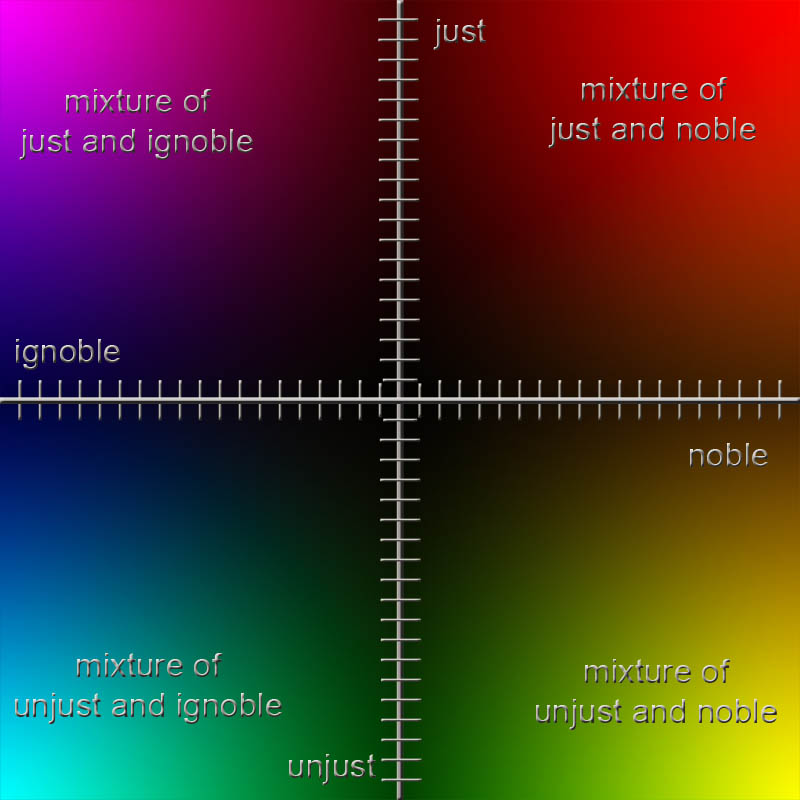
We can see the color purple as blend of ignoble and just, red-orange as a blend of just and noble, yellow-green as a blend of noble and unjust and blue-green as a blend of ignoble and unjust. For the record, I certainly am not trying to say there is a relationship of ignobility and injustice with the color blue-green! This example is just a tool to help us with our own concept of visualizing a word-plane. However, we could create a different but, in my opinion, limited set of color metaphors for noble/ignoble and just/unjust. Or we could look at our color example as adjectives on their own merit. This method would automatically help us see them as metaphors. Example: She was red hot. He had a blue day. He was so green he did not know what was happening. Multiplying adjective word-axes together instantly create metaphors.
2.2. Word-coordinate Pairs: We have witnessed a word-axis with different values
of an antonym pair along a particular axis 'x' or 'y' in one dimension.
(See figure 3) We also have seen a word-plane with values of two
antonym pairs along two axes 'x' and 'y' in two dimensions. (See
figure 10) Furthermore, we can have word-cubes along the x, y,
and z-axes in the third and word-hypercubes in the fourth dimension
or we can have antonymic pairs in innumerable dimensions. There
is no limit to the dimensional palette for our expressions. Each
antonym word-pair adds a new spatial dimension to our expressive
construction.
Let us talk about the spatial accuracy in defining the location
of words in space. Once again, let us look at figure 10 and notice
the antonym word pairs, just/unjust and noble/ignoble. However,
let us focus our attention to the word-axis just/unjust. We know
that we have defined a one-dimensional word-axis with different
values of just and unjust but we do not know exactly where each
of the words is located along the axis. We have no quantitative
value for just or unjust. However, we do have a qualitative value
and we know that the word exists somewhere on the axis. What is
most important to us in verbogeometry is not the value as such,
but the spatial relationship of the values to each other in space.
Because the value or the meaning of a word is relative to the
context in which it is used, each viewer individually creates
his or her own context for meaning. Therefore, exact quantification
of the word or its location in space is not possible. However,
in some cases, it may be possible to restrict the context to a
level where repeatable correlations exist, but those studies are
more akin to denotation for the purpose of science. Scientific
experimentation "proves" the equation to be mathematically
correct and workable within a range of acceptability. In other
words, experimental data defines viability of the relationships
between the concepts in a scientific equation. On a side note:
(When scientific equations are in the intuitive stages of development,
there may be an argument to claim that they are in the realm of
art, I personally might accept this view if it were not for the
fact that their intention is not to make art.) In verbogeometry,
we construct equations based on relationships between the qualities
of our experiences to evoke meaningful aesthetic expressions of
which most are connotative but some may be denotative.
Let us get back to the Cartesian coordinate system for a moment
and reiterate the idea of coordinate pairs. A point on a two dimensional
coordinate system would have values for x and y and would be expressed
as such: (x,y) (see figure 1.) A point on a three-dimensional
axis system would have values for x, y and z and would be expressed
as (x,y,z). A four dimensional point would be expressed as (x,y,z,w)
in the fifth dimension as (x,y,z,w,v) etc.
Before we get into multidimensional word-axes let just look at
a simple two-dimensional word-plane with two word-axes. (see figure
12.)
Figure 12 
The vertical axis is a synonym word-pair of praise and punishment and the horizontal axis is a synonym word-pair of love and hate. It is very important to realize that not only does the words love and hate define the identity of the horizontal or x-axis they also hold conceptual points in space along the axis and the same for praise and punishment with respect to the y-axis. The words which are conceptual points in space define a metaphoric value along its respective axis and can be notated as a coordinate pair similar to (x,y) So you may ask what would a coordinate word-pair look like? Let us look at the two points identified as point 1 or P1(love,praise) and point 2 P2(hate,punishment) (see figure 13.)
Figure. 13 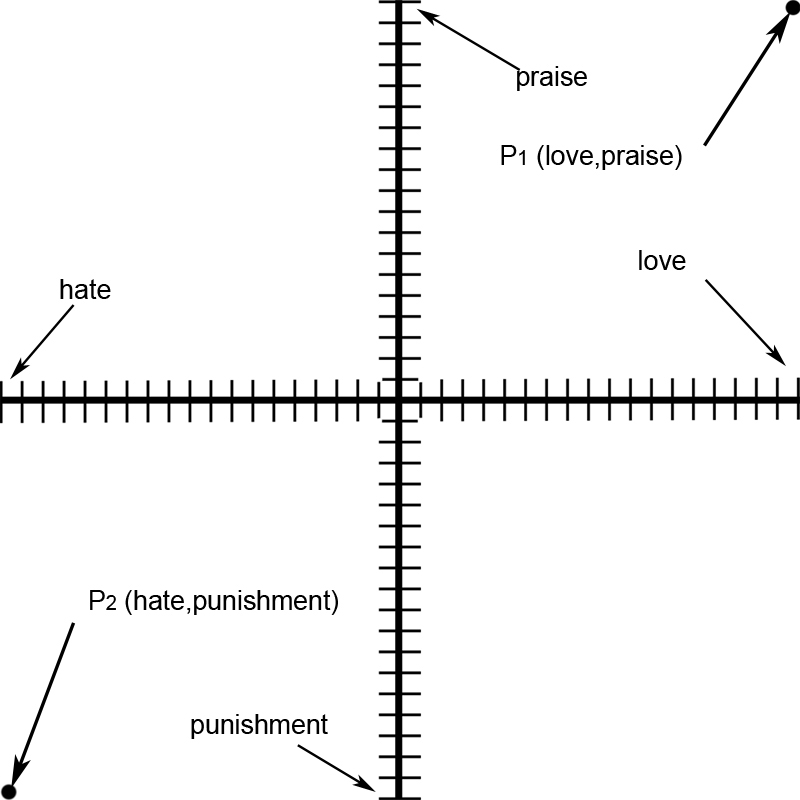
2.3. Midpoint Formula in
Verbogeometry: Any analytic geometry equation
can use coordinate word-pairs instead of numbers to express poetic
forms. Let us use the midpoint formula to express the exact point
between the two points P1(praise,love) and P2(punishment,hate)
from figure 13. Before we look at coordinate word-pairs let us
refresh the use of the midpoint formula in analytic geometry.
To find the midpoint between two points on a Cartesian coordinate
system we add the x coordinates together and divide by 2 to find
the x value for the midpoint and we also add the y coordinates
together and divide by 2 to find the y value for the midpoint
or
(x1 + x2)/2 = x0 and (y1 + y2)/2 = y0.
Lets look at an example of finding the midpoint P0 between the
points P1(-14-15) and P2(12,11) utilizing the midpoint formula.
x1 = -14 and x2 = 12 so substituting our numbers in the variables
of the equation (x1 + x2)/2 = x0 we get (-14 + 12)/2 = -1 also
y1 = -15 and y2 = 11 so substituting our numbers in the variables
of the equation (y1 + y2)/2 = y0 we get (-15 + 11)/2 = -2 therefore:
P0 = (-1,-2) (see figure 14.)
Figure. 14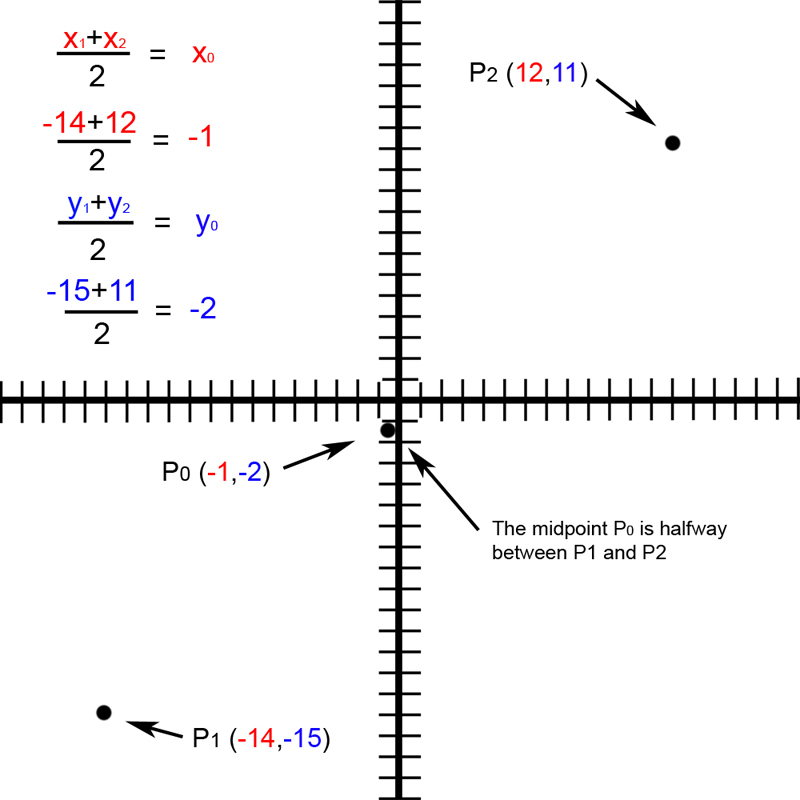
Let us now take a different approach and replace the numeric variables in the midpoint equation with the words/concepts of love, hate, praise and punishment. We will use the form of coordinate word-pairs P2(love, praise) and P1(hate, punishment). The midpoint formula now shows us that P0(x0, y0) will be formed by the substitution of (x1 + x2)/2 = x0 with (love + hate) = x0 and (y1 + y2)/2 = y0 with (hate + punishment) = y0. Now we have expressed the exact point between love, praise and hate, punishment. (see figure 15.)
Figure. 15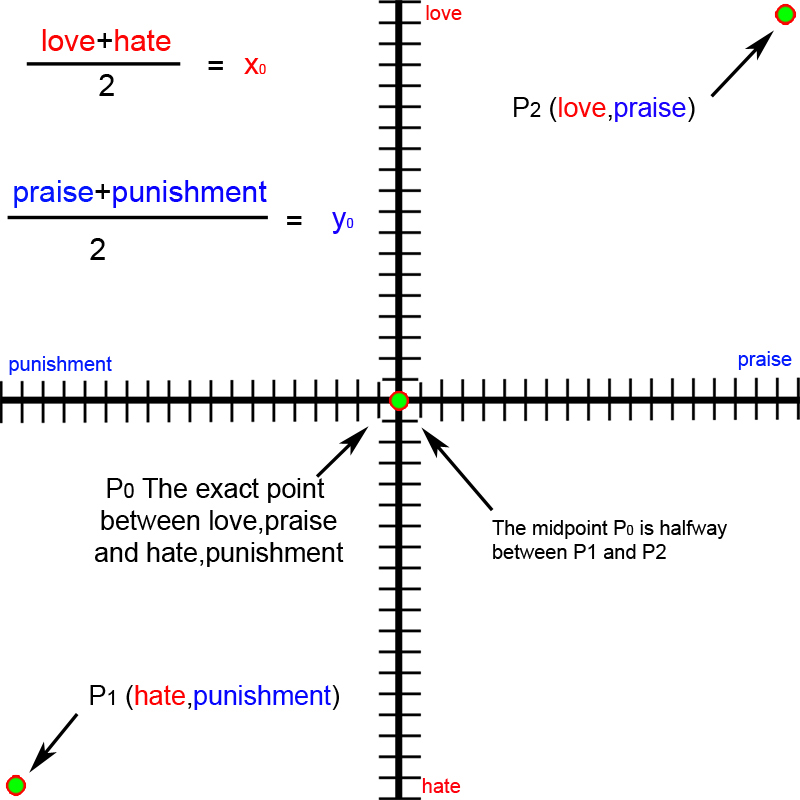
2.4. Verbogeometry with Trigonometry: First let us solve a pertinent traditional trigonometric problem, which requires a solution for an angle. Let us make 'theta' the variable of the angle in question. The tangent of a right triangle is defined as the ratio of the side opposite the angle 'theta' to the side adjacent to the angle 'theta'. If we call the side opposite distance "y" and the side adjacent as distance "x" we then arrive at tan (angle theta) = y/x (See figure 16)
Figure 16.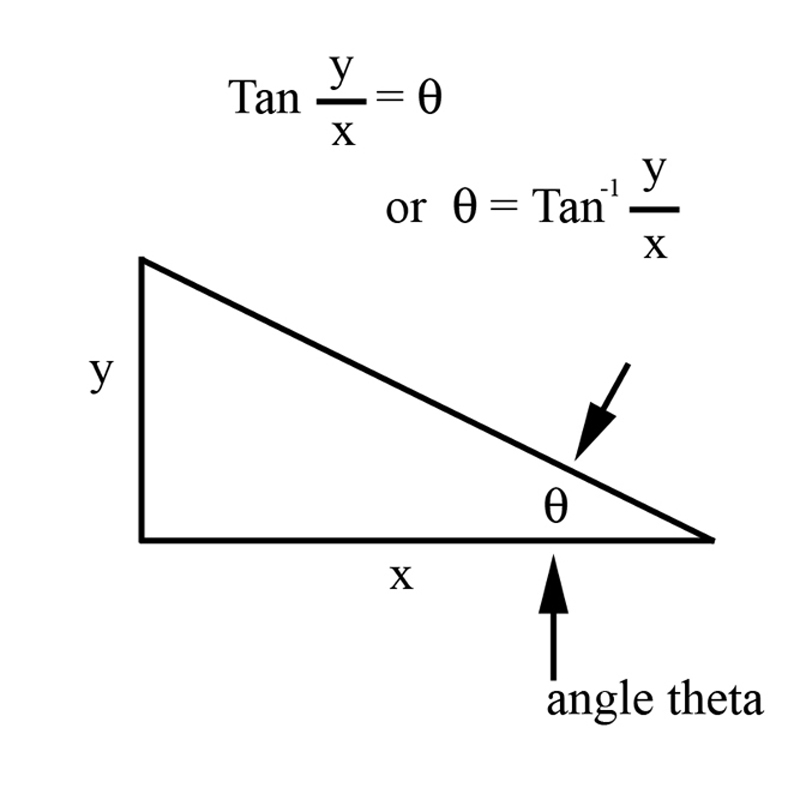
It also follows that if we know the distance of two sides of a right triangle we can find all the angles. Let us look at an example with the side opposite angle theta being 3 and the side adjacent to angle theta being 4 and. Let us now solve for the angle theta. We know that y/x = tan (theta) so it follows ¾ = tan (theta). To uncover the value of theta, we must take the inverse tangent of ¾. Symbolically this is stated as "theta = inverse tan(y/x)" or approximately 36.87 degrees (See figure 17).
Figure. 17 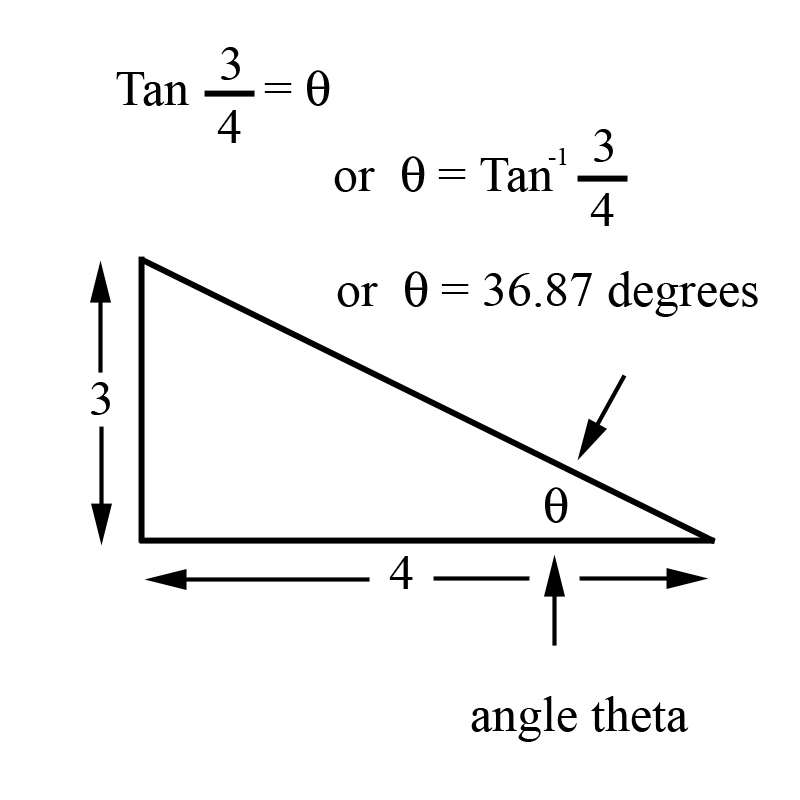
In general, to reveal the angle after you have calculated the
value for the tangent of y/x, your choice is to find the angle
on a trigonometric table (old method) or you plug the values in
on a hand held calculator.
Now let us look at a similar expression using verbogeometry and
looking for the value of angle theta. This time we define the
y distance as the difference between the concepts of barren and
infertile (think number-line again) and let us define the x distance
as the difference between the concepts of infertile and fertile.
(See figure 18)
Figure. 18
If we want to know the angle of theta we have to take the inverse tangent of y/x or the inverse tangent of (barren - infertile)/(fertile - infertile) (see figure 18)
2.5. Prismatic Structures in Verbogeometry: Notice that 'barren and fertile' is a complex antonym and 'fertile and infertile' is a simple antonym as previously defined. This is interesting because we can see that there exists in verbogeometry a geometric construction where a line expressed as a simple antonym is normal (90 degrees) to a plane containing all of the complex antonyms related to the line which is expressing the simple antonym. To illustrate this idea lets look again at the relationship between the simple antonyms 'fertile' and 'infertile' and the synonyms 'barren', 'fruitless', 'unproductive', 'sterile', 'impotent' which reside on the plane that is normal (90 degrees) to the line created by the simple antonyms. Furthermore you can draw lines from all of the synonyms back to the complex antonym 'fertile'. (See figure 19)
Figure. 19 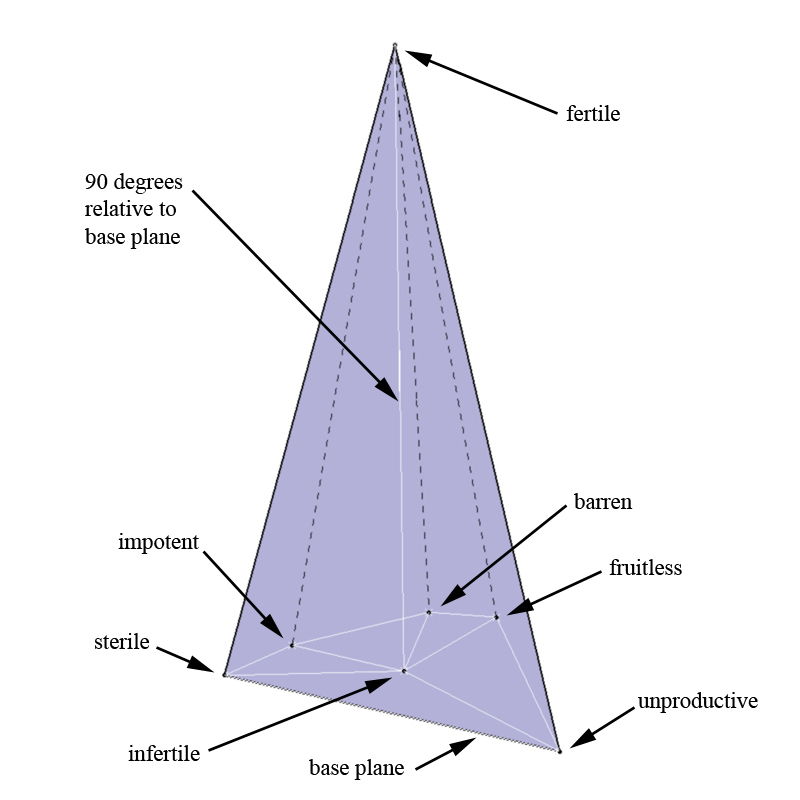
This idea also lends itself to prismatic structures where we have a group of parallel simple antonyms whose endpoints construct polygonal faces on two parallel synonym-planes. (See figure 19) Example: Let us define one synonym plane containing the words 'pleased', 'content', 'affected', 'satisfied', 'enchanted' and 'sympathetic'. The other plane contains the following simple antonyms for the previous group of synonyms: 'displeased', 'discontent', 'disaffected', 'dissatisfied', 'disenchanted' and 'unsympathetic'. Due to the synonyms of one plane have corresponding simple antonyms which create lines 90 degrees from the synonym-plane then the simple antonyms are synonyms of each other and reside on their own individual synonym plane and because the lines are 90 degrees to each other the planes must be parallel. The former verbiage is a lot easier to understand visually (See figure 20)
Figure. 20 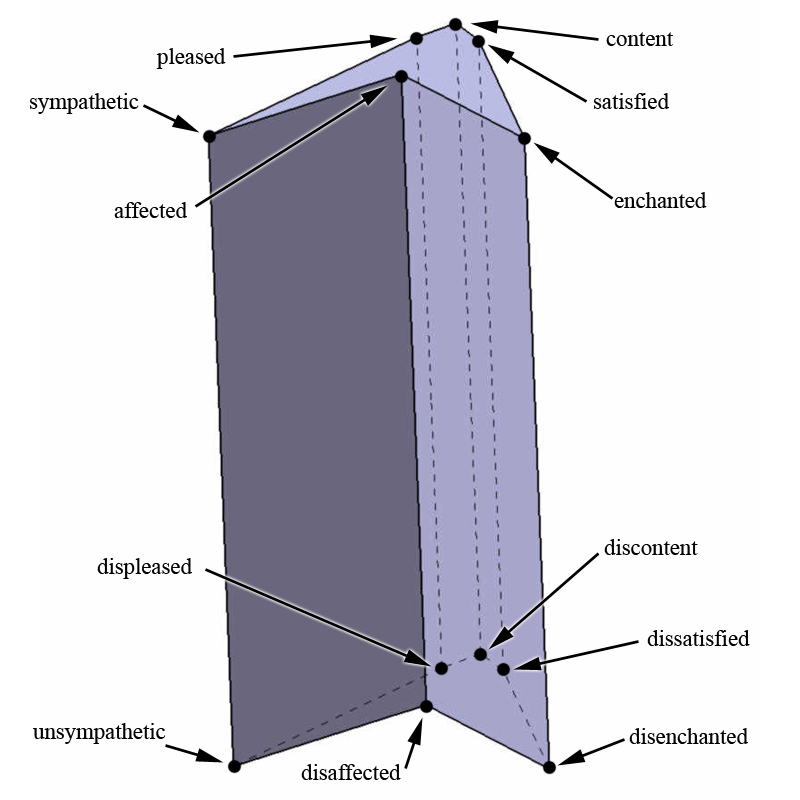
On a side note: Everything that we have been talking about up to this point has been viewed in Euclidian space. Not much time has been spent exploring verbogeometry outside of Euclidian space. However, I see that there can be a lot more thought evolving models of verbogeometry in other spaces. For example, Instead of viewing antonyms and all the varying meanings spread out across a number-line, we may think of the antonyms as magnetic dipoles. Furthermore, all the varying meaning between them is analogous to a magnetic flux. Yet again, another view may be looking at the antonyms residing at the endpoints of a major axis of a three dimensional ellipsoid and the varying meanings reside on the surface of the ellipsoid. (See figure 21)
Figure. 21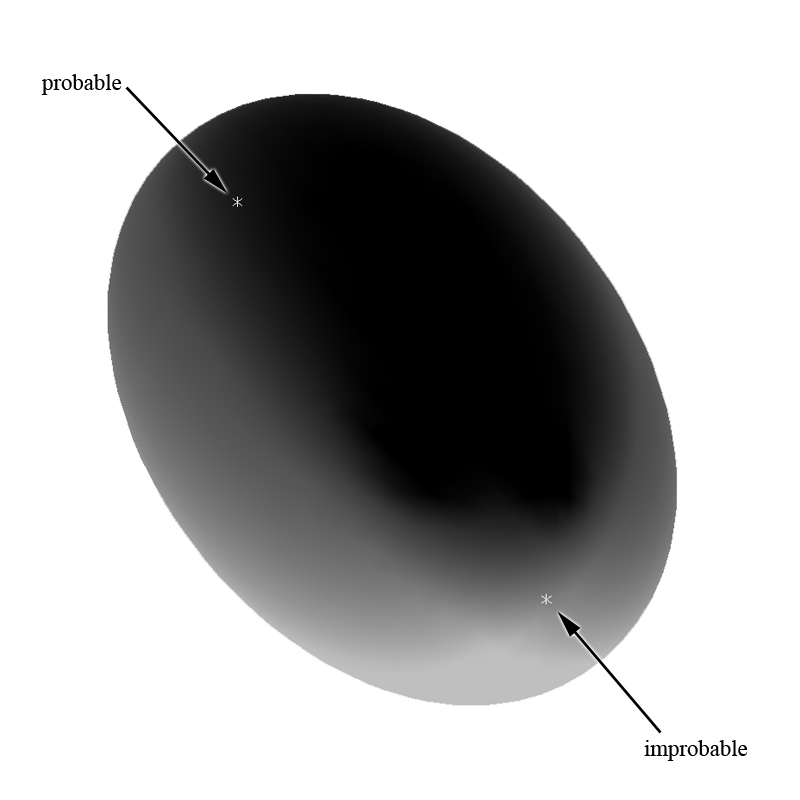
Figure 22 shows an ellipsoidal flux-like paradigm for the previous
prismatic structure. (See figure 20)
Figure. 22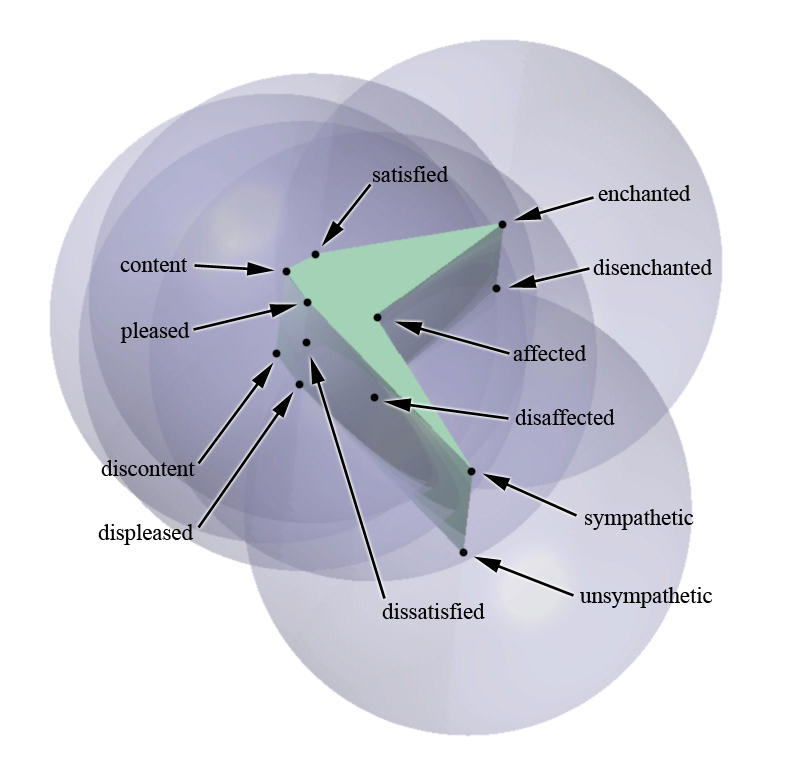
Figure23 shows an unlabeled side view
Figure23 
It may be easier to see the ellipse structure if it was wireframe
(See figure 24)
Figure. 24 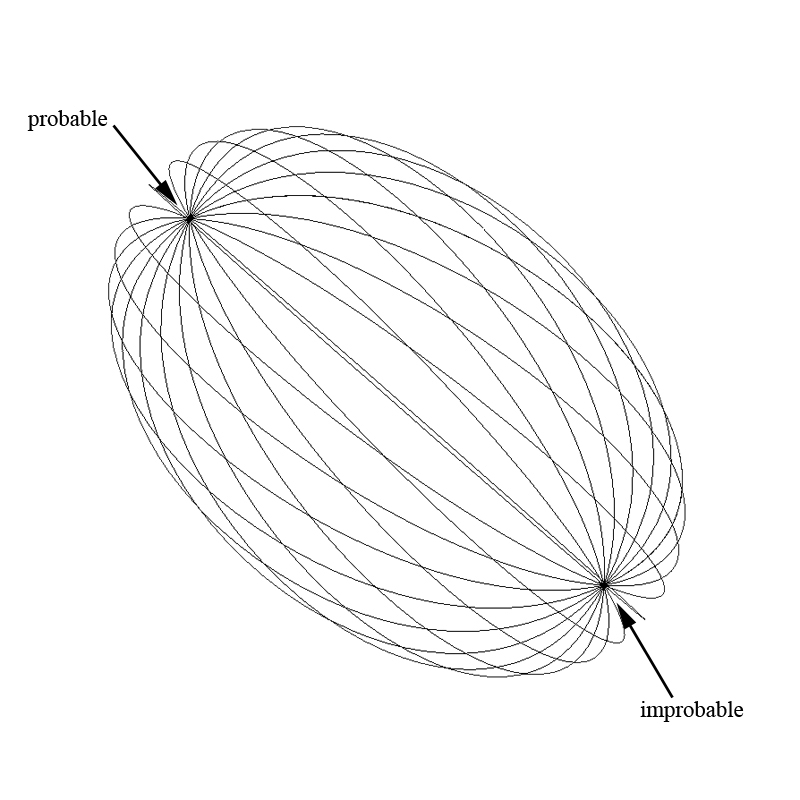
Figure 25 shows 5 parallel word axis in a wireframe structure
Figure 25
2.6. The Distance Formula and Pythagorean Theorem: The distance formula uses the Pythagorean Theorem to calculate distances on the Cartesian coordinate system. The Pythagorean Theorem says that the square of the hypotenuse of a right triangle is equal to the sum of the squares of it sides. (see figure 26)
Figure. 26 
solve for c and we get the following see figure 27
Figure. 27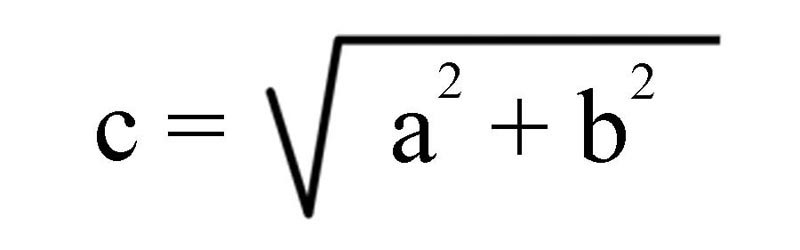
Let us plot two points on a two-dimensional axis system P1(-9,10) and P2(4,3) and If we draw a lines between the points and lines parallel to the axes we can obtain a right triangle. (see figure 28)
Figure. 28 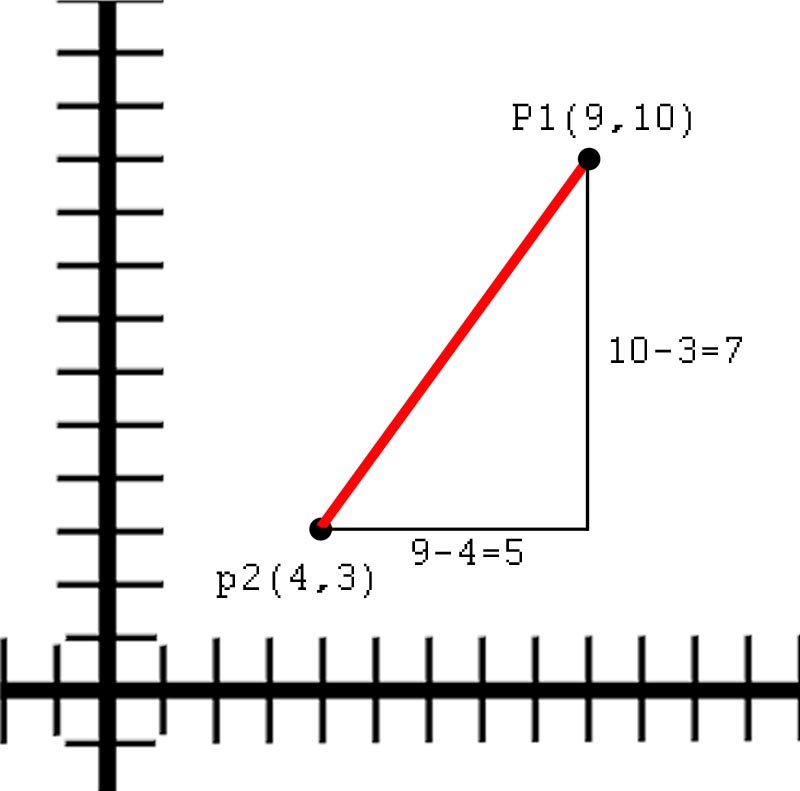
To solve the length of the hypotenuse we first find the difference between the x values and the y values to create the sides of the triangle then we plug the values into the Pythagorean Theorem. x value is 9 - 4 = 5 and the y value is 10 - 3 = 7 Now we plug it to the equation and we get the expression in figure 29
Figure 29
The distance or length of the hypotenuse would be the square root
of 74 or approximately 8.602
The distance formula is thus:
Given two points (x1,y1) and (x2,y2) (see figure 30)
Figure 30 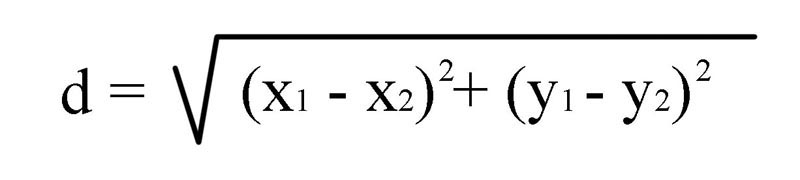
Now what we have been looking at up till now has been in two-dimensions
but we can also express a distance in many dimensions. Let us
look at two points in three dimensions.
P1(x1,y1,z1) P2(x2,y2,z2)
If we were to put these two points into the distance formula it
would look like what is shown in figure 31
Figure 31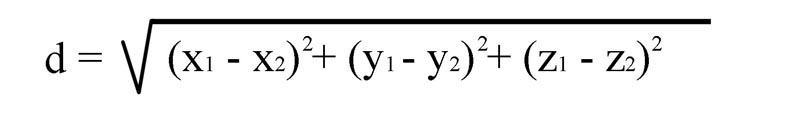
It is evident that we can use the distance formula in uncountable
dimensions all we have to is to add another dimensional term to
the formula for every dimension we wish to express.
2.7. Distance Formula and
Verbogeometry.
As we have seen, to calculate
the distance between two points, we need to describe our points
by its coordinates using the nomenclature of the coordinate pair.
Let me reiterate, describing a point in verbogeometry is no different
from numerical coordinates except we use words. Lets look again
at the example in figure 15 where we used the midpoint formula
to find the exact point between the points: P1(love,praise) and
P2(hate,punishment) but instead of putting them in the midpoint
formula lets put them in the distance formula. (See figure 32)
Figure 32 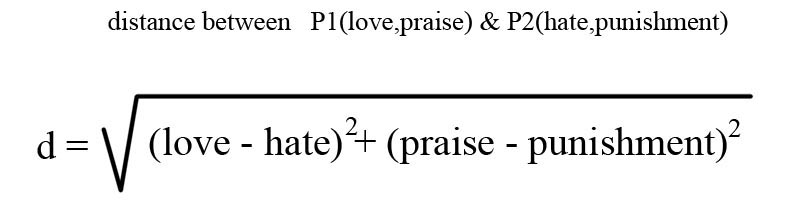
Here we have an expression for the distance between the points
P1(love,praise) and P2(hate,punishment) in two dimensions. But
we can also use verbogeometry in any number of dimensions including
hyper-dimensions. But before we look at hyper dimensional verbogeometry
lets look at another example which we will express in the third
dimension. The following example uses a three dimensional Cartesian
coordinates system with 3 simple antonym word-axes. (See figure
33) The first axis is noble / ignoble the second axis is just
/ unjust and the third axis is loyal / disloyal.
Figure 33 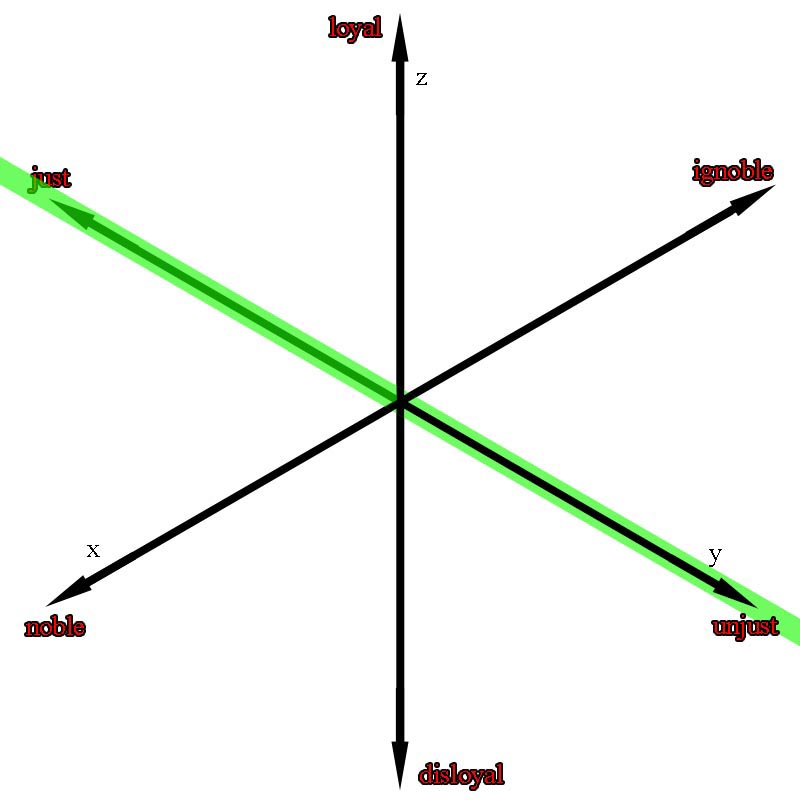
Now lets look at the expression for the distance between the points P1(noble,just,loyal) and P2(ignoble,unjust,disloyal) see figure 34
Figure 34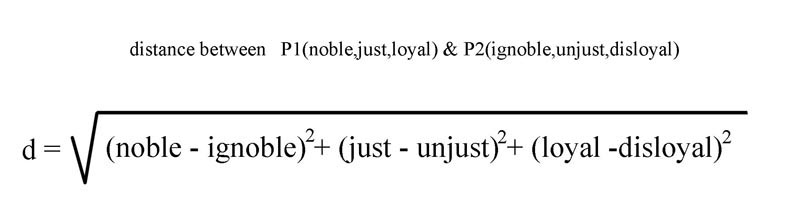
Notice the green line in figure 33 is the visual representation for the mathematical expression above. However, it would be much easier to visualize if we were able to rotate the axis. Figure 33 is an isometric view, which I chose to use because it is best for viewing the axis but unfortunately at the expense of viewing the spatial orientation of the green line.
Now let us look at verbogeometry in a hyper-dimension. Let us look at the distance formula used in seven dimensions:
Figure 35 shows the mathematical poem 1+1+1+1+1+1+1+1 =1 This is a metaphorical piece that creates a metaphoric path from the concept of confusion, to where seven deities meet. The piece uses the analytic geometry distance formula in a seven dimensional space where each dimension is a gradation from confusion to a point where a deity exists.

Here is a detail:
Figure 35
Lets look at the coordinate pairs for these two points P1(confusion,
confusion, confusion, confusion, confusion, confusion, confusion)
and P2(Allah,Buddha,Jesus,Spider woman,Vishnu,Yahweh,Zeus)
In conclusion what I have shown is scratching the surface of the
possibilities of verbogeometry. Verbogeometry can be taken in
vast directions that I have not covered or will be able to cover.
I hope, in the future, more people join in to explore the possibilities
of verbogeometry.
Kaz Maslanka
San Diego, California
February 3, 2006